Выделение эрмитовых матриц в качестве особого класса обусловлено следующими причинами:
| - | проблема собственных значений для эрмитовых матриц значительно проще, чем для матриц общего вида, так как |
| 1. | собственные значения эрмитовых матриц являются вещественными; |
| 2. | собственные векторы эрмитовых матриц могут быть выбраны ортогональными и образуют полную систему; |
| 3. | характеристические многочлены главных подматриц эрмитовой матрицы обладают свойствами последовательности Штурма; |
| 4. | задача вычисления собственных значений эрмитовой матрицы очень устойчива в смысле абсолютных погрешностей: теоретически абсолютная погрешность любого собственного значения возмущенной эрмитовой матрицы не превосходит спектральной нормы возмущения (если возмущение тоже эрмитово); |
| 5. | алгоритмы, учитывающие специфику эрмитовых матриц, требуют меньше машинного времени и памяти; |
| - | наибольшее число приложений связано именно с эрмитовыми (вещественными симметричными) матрицами. |
Процесс решения полной проблемы собственных значений для полной эрмитовой (вещественной симметричной) матрицы состоит из следующих этапов:
| - | приведение эрмитовой (симметричной) матрицы A к вещественному симметричному трехдиагональному виду T с помощью унитарного (ортогонального) преобразования подобия T = U*AU (T = UTAU); информация о выполненных преобразованиях (о матрице U) запоминается, если требуется вычислить не только собственные значения матрицы A, но и ее собственные векторы; |
| - | вычисления собственных значений и (если нужно) собственных векторов вещественной симметричной трехдиагональной матрицы T с помощью QL - алгоритма; |
| - |
восстановление собственных векторов исходной эрмитовой
(симметричной) матрицы по вычисленным собственным
векторам трехдиагональной матрицы T
X = UY ,где X - матрица собственных векторов исходной матрицы A, а Y - матрица собственных векторов матрицы T. |
Перечисленные преобразования входят в состав подпрограмм AEH1C (AEH1R), AEH2C (AEH2R).
При решении частичной проблемы собственных значений для эрмитовой вещественной симметричной матрицы заданная матрица также предварительно преобразуется в вещественную симметричную трехдиагональную матрицу. Затем методом деления отрезка пополам (методом бисекции) вычисляются собственные значения преобразованной матрицы, принадлежащие заданному интервалу. Если же ищутся дополнительно соответствующие этим собственным значениям собственные вектора, то применяется метод обратной итерации, затем по собственным векторам трехдиагональной матрицы восстанавливаются собственные векторы исходной эрмитовой (вещественной симметричной) матрицы. Перечисленные преобразования реализованы в подпрограммах AEH4R, AEH4C, AEH3R и AEH3C.
Рассматриваемый подраздел Библиотеки численного анализа для вещественных симметричных матриц предусматривает две формы хранения исходных матриц: в виде задания всех элементов матриц в полном квадратном массиве и в виде одномерного массива, в котором помещены элементы нижнего треугольника по строкам (в так называемой компактной форме).
Перечислим теперь некоторые подклассы эрмитовых матриц, для которых решение проблемы собственных значений осуществляется с помощью специальных подпрограмм, учитывающих специфику этих подклассов.
Вещественная симметричная ленточная матрица задается в виде прямоугольной матрицы размерности [n * m], где n - порядок исходной матрицы, m - число нижних кодиагоналей, включая главную. Столбцы этой матрицы представляют собой нижние кодиагонали исходной матрицы, причем в последнем столбце задается главная диагональ.
Для вещественной симметричной ленточной матрицы известен алгоритм приведения к симметричному трехдиагональному виду, сохраняющий ее ленточную старуктуру в течение всего процесса приведения. Остальные этапы решения проблемы собственных значений (полной и частичной) для матриц этого подкласса - те же, что и для полной вещественной симметричной матрицы. Имена соответствующих подпрограмм - AEB0R, AEB1R, AEB2R, AEB3R.
Частичная проблема собственных значений для матриц рассматриваемого подкласса может быть решена еще и другим способом. Можно метод бисекции и метод обратной итерации применить непосредственно к исходной симметричной ленточной матрице, не приводя ее предварительно к трехдиагональному виду. Имена соответствующих подпрограмм - AEB5R, AEB6R. Этот способ решения частичной проблемы будет более предпочтителен, когда число требуемых собственных значений и собственных векторов незначительно и ширина ленты невелика.
Для решения полной проблемы собственных значений вещественной симметричной трехдиагональной матрицы используется QL - алгоритм с неявным сдвигом, а для решения частичной проблемы - метод бисекции и метод обратных итераций.
Вещественные симметричные трехдиагональные матрицы представляют в памяти машины в виде двух векторов, в одном из которых располагаются диагональные элементы, в другом - поддиагональные элементы. Другая форма хранения - двумерный массив размерности [n * 2] - соответствует стандартной форме хранения для вещественной симметричной ленточной матрицы.
Для решения спектральных задач для симметричных разреженных или регулярной стурктуры матриц большого порядка удобен метод Ланцоша. Этот метод использует исходную матрицу только в операциях умножения матрицы на вектор, поэтому информацию о матрице можно задавать в виде подпрограммы умножения матрицы на вектор, в которой пользователь может максимально учесть специфику матрицы.
Для решения различных спектральных задач используются различные модификации метода Ланцоша.
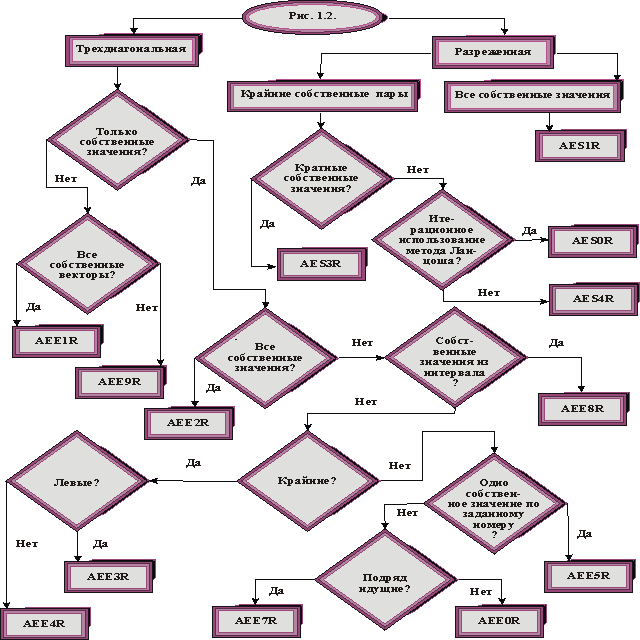
Простой метод Ланцоша используется для вычисления всех собственных значений (без учета их кратности) (подпрограмма AES1R), метод Ланцоша с выборочной ортогонализацией - для вычисления нескольких крайних собственных пар (подпрограммы AES4R, AES0R), блочный метод Ланцоша с выборочной ортогонализацией - для вычисления нескольких крайних собственных пар матриц, имеющих кратные собственные значения (подпрограмма AES3R). При этом подпрограммы AES3R и AES0R используют метод Ланцоша итерационным образом.
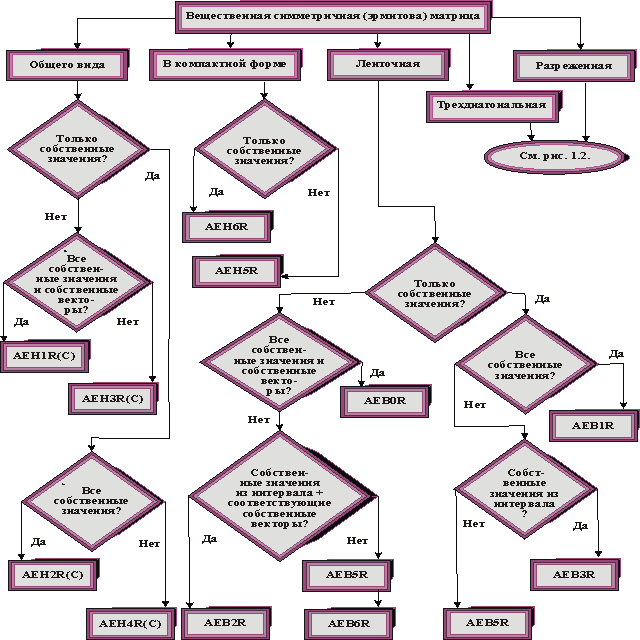
Информация о всех подпрограммах рассматриваемого подраздела, предназначенных для эрмитовых матриц, собрана на рисунках 1.1 и 1.2 и оформлена в виде дерева решений, где указаны названия подпрограмм. Для того чтобы не рисовать отдельное дерево для комплексных эрмитовых матриц, на рисунках 1.1 и 1.2 в скобках после имени подпрограммы для вещественной симметричной матрицы указывается, как меняется последний символ (или 2 последних символа) в названии подпрограммы для случая комплексной эрмитовой матрицы.
| Рис. 1.1 и 1.2 | Дерево решений для выбора программы решения линейной проблемы собственных значений для вещественной симметричной (эрмитовой) матрицы. |