Собственные значения неэрмитовых матриц могут быть очень чувствительны к малым изменениям элементов матрицы. Неэрмитова матрица может иметь нелинейные элементарные делители, в этом случае собственные векторы неэрмитовой матрицы не порождают полного пространства.
Вычислительная проблема считается плохо обусловленной, если вычисляемые величины значительно меняются при малом изменении входных данных и, наоборот, хорошо обусловленной, если малым изменениям входных данных соответствуют малые изменения вычисляемых величин. Для характеристики такой чувствительности используются числа обусловленности. В качестве чисел обусловленности для проблемы собственных значений матрицы A (в предположении λi ≠ λj при i ≠ j ) Уилкинсон предложил использовать коэффициенты перекоса ci = || xi || || yi || / | xiT yi |, где xi, yi - собственные векторы матриц A и A*, соответствующие собственным значениям λi и λi. Пусть λ iº , x iº собственные значения и соответствующие собственные векторы возмущенной матрицы Aº = A + Δ, где || Δ || 2 мала; пусть || x i || = || x iº || = 1, тогда с точностью до членов второго порядка имеют место оценки [ 2 ]:
| λºi - λ i | < ci || Δ || 2 ,
|| xºi - x i || 2 < || Δ || 2 ∑ cj / | λ i - λ j | .
j≠1
Для эрмитовой матрицы все коэффициенты перекоса равны 1, для
неэрмитовой матрицы некоторые ci могут быть величинами
порядка 1, а некоторые ci могут быть очень велики.
Существуют неэрмитовы матрицы, для которых все ci велики,
т.е. все собственные значения плохо обусловлены.
В то же время известен подкласс неэрмитовых матриц, для
которого все ci равны 1.
Этим свойством обладают нормальные матрицы, т.е. те, для
которых выполнено равенство AA* = A*A.
Для определения обусловленности всех собственных значений берется
min K (DX) ,
D
где X - матрица собственных векторов, т.е. XAX - 1 = diag (λ1, ..., λn), K (Z) = || Z || || Z - 1 || - спектральное число обусловленности, а D пробегает множество диагональных матриц.
Установлено, что всякая матрица, имеющая плохую обусловленность для проблемы собственных значений, близка к матрице, имеющей кратные собственные значения (сама матрица может при этом иметь хорошо разделенные собственные значения).
Так как все вычисления производятся в условиях ошибок округления, то нельзя точно определить, имеет матрица нелинейные делители или нет. Поэтому обычно ищется полное число собственных векторов, равное порядку матрицы.
Проанализировав вычисленные собственные векторы и обнаружив, что есть почти параллельные, можно сделать вывод о существовании нелинейных элементарных делителей.
Процесс решения полной проблемы собственных значений комплексной (вещественной) матрицы общего вида состоит из следующих этапов:
| - | предварительное масштабирование (балансирование) исходной матрицы A с целью уменьшить влияние ошибок округления в последующих вычислениях (B = D - 1 AD, D - диагональная); |
| - |
приведение полученной в результате масштабирования матрицы B к
верхней почти треугольной форме
T = U* BU (T = UT BU) ; |
| - | вычисление собственных значений верхней почти треугольной матрицы T (они совпадают с собственными значениями исходной матрицы A) с помощью QR - алгоритма; |
| - | вычисление матрицы Y собственных векторов матрицы T; |
| - | восстановление матрицы Z собственных векторов матрицы B (Z = UY); обычно сама матрица Y не вычисляется, а вычисляется сразу Z; |
| - | восстановление матрицы X собственных векторов исходной матрицы A (X = DZ). |
В подпрограмме AEG1C (AEG1R) реализованы все перечисленные выше этапы, кроме первого и последнего. Поэтому перед применением этой подпрограммы рекомендуется воспользоваться подпрограммой масштабирования AMB1C (AMB1R), тогда после применения AEG1C (AEG1R) необходимо будет обратиться к подпрограмме AMB1CC (AMB1RR) восстановления собственных векторов исходной матрицы по собственным векторам матрицы, полученной в результате масштабирования.
В подпрограмме AEG2C предварительно масштабирование исходной матрицы также не осуществляется, поэтому перед обращением к подпрограмме AEG2C следует воспользоваться подпрограммой AMB1C.
Для решения частичной проблемы собственных значений неэрмитовой матрицы в рассматриваемом подразделе Библиотеки нет подпрограмм. Если же собственные значения известны, то методом обратных итераций можно вычислить отдельные собственные векторы, соответствующие указанным собственным значениям.
Матрица A называется верхней (нижней) матрицей Хессенберга, если ai j = 0 при i > j + 1 ( j > i + 1).
В рассматриваемом подразделе Библиотеки имеются подпрограммы решения проблемы собственных значений для комплексной и вещественной верхних матриц Хессенберга. Для решения полной проблемы собственных значений используется QR - алгоритм (подпрограммы AET1R, AET2R, AET1C, AET2C). Для решения частичной проблемы собственных значений для матрицы Хессенберга подпрограмм в данном разделе нет, но если собственные значения уже вычислены, то с помощью метода обратных итераций можно вычислить отдельные собственные векторы, соответствующие указанным собственным значениям (подпрограммы AET3R и AET3C). Так же, как и в случае матрицы общего вида, полезно провести предварительное масштабирование матрицы Хессенберга, используя подпрограмму AMB1C (AMB1R). Тогда после вычисления собственных векторов промасштабированной матрицы собственные векторы исходной матрицы могут быть восстановлены с помощью подпрограммы AMB1CC (AMB1RR).
Трехдиагональная матрица A с главной диагональю ( a1, a2, ... , an ), верхней кодиагональю ( b2, ... , bn ) и нижней кодиагональю ( c2, ... , cn ) называется матрицей Якоби, если все ее диагональные элементы вещественные, а внедиагональные удовлетворяют условию
bi ci > 0 , i = 2, ..., n .
Понятно, что bi и ci могут быть и комплексными.
Любая матрица Якоби с помощью диагонального преобразования подобия может быть приведена к вещественному симметричному трехдиагональному виду
T = D - 1 AD .
При этом диагональные элементы матриц T и A совпадают, а элементы диагональной матрицы D = diag (d1, ..., dn) и внедиагональные элементы m2, ..., mn матрицы T могут быть определены из соотношений
mi = ( bi ci ) 1/2 , d2i = d2i -1 ci / bi , i = 2, ..., n
(d1 - любое ненулевое значение).
Такое приведение осуществляется в подпрограммах AFJ0R и AFJ0C.
Для вещественной матрицы Якоби решение полной проблемы собственных значений и вычисление собственных значений, принадлежащих заданному интервалу, и (если нужно) соответствующих собственных векторов выполняется с помощью подпрограмм AEJ2R, AEJ1R, AEJ3R, AEJ4R.
Для комплексной матрицы Якоби в данном подразделе нет
специальных подпрограмм решения проблемы собственных значений. Для
такой матрицы можно сначала использовать AFJ0C, а затем
какую - либо подпрограмму решения проблемы собственных
значений для трехдиагональной матрицы.
Если при этом нужны и собственные векторы, то необходимо
восстановить их по собственным векторам трехдиагональной матрицы
согласно формуле (4) из п.1, взяв в качестве P диагональную
матрицу D, полученную в результате работы подпрограммы AFJ0C.
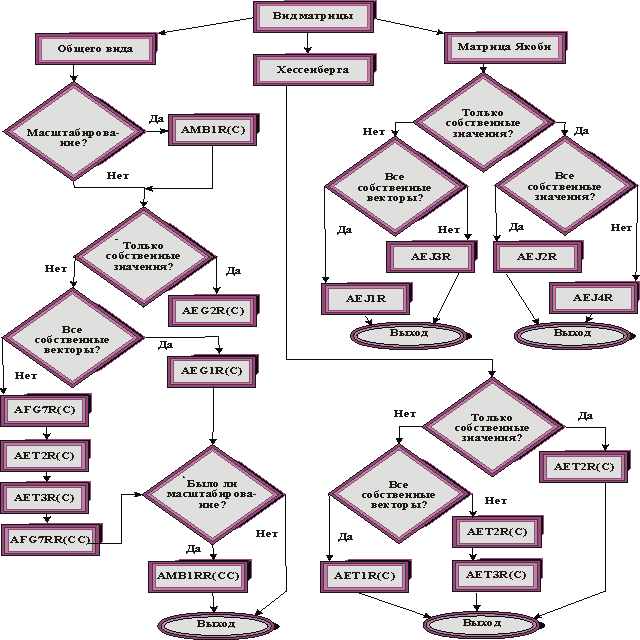
Информация о всех подпрограммах, решающих проблему собственных значений для неэрмитовых матриц, оформлена в виде дерева решений на рис.2, где указаны имена подпрограмм. Для того чтобы не рисовать отдельное дерево для комплексных матриц общего вида, на рис.2 в скобках после имени подпрограммы для вещественной матрицы указывается, как меняется последний символ (или два последних) в названии подпрограммы для случая комплексной матрицы.

| Рис. 2. | Дерево решений линейной проблемы собственных значений для вещественных (комплексных) матриц общего вида. |
На рис.2 фигурируют имена подпрограмм AMB1RR (CC) и AFG7RR (CC), которые являются вспомогательными и для которых поэтому в рассматриваемом подразделе Библиотеки нет подробных описаний. Приведем здесь сведения, необходимые для использования этих подпрограмм (краткие описания). ( Тексты подпрограммы AMB1RR и ее версий на Фортране содержатся в файлах: amb1rr.zip , amb1dd.zip , amb1cc.zip , amb1pp.zip .; на языке Си - в файлах: amb1rr_c.zip , amb1dd_c.zip , amb1cc_c.zip , amb1pp_c.zip . Тесты к этим подпрограммам на Фортране содержатся в файлах: tamb1rr.zip , tamb1dd.zip , tamb1cc.zip , tamb1pp.zip ).
Подпрограмма: AMB1RR
Назначение
Восстановление собственных векторов вещественной матрицы общего вида по собственным векторам матрицы, полученной из исходной в результате ее масштабирования с помощью подпрограммы AMB1R
Использование
SUBROUTINE AMB1RR (NM, N, LOW, IGH, SCALE, M, Z)
Параметры
| NM - | число строк двумерного массива Z, указанное при описании этого массива в вызывающей подпрограмме (тип: целый); |
| N - | порядок матрицы A, собственные векторы которой требуется вычислить, N ≤ NM (тип: целый); |
| LOW - IGH | простые переменные, выходные параметры подпрограммы AMB1R (тип: целый) (см. описание 4 - го и 5 - го параметров подпрограммы AMB1R); |
| SCALE - | вещественный вектор длины N, выходной параметр подпрограммы AMB1R (см. описание 6 - го параметра подпрограммы AMB1R); |
| M - | число столбцов массива Z (тип: целый); |
| Z - | вещественный двумерный массив размерности NM на M, в столбцах которого на входе в подпрограмму содержатся вещественные и мнимые части собственных векторов матрицы C, полученной в результате масштабирования исходной матрицы A с помощью подпрограммы AMB1R, а на выходе из подпрограммы, - соответственно, вещественные и мнимые части соответствующих собственных векторов матрицы A (используются только первые N компонент каждого столбца массива Z) |
Версии
| AMB1DD - | восстановление собственных векторов вещественной матрицы общего вида по заданным с двойной точностью собственным векторам матрицы, полученной в результате масштабирования исходной матрицы с помощью подпрограммы AMB1D |
| AMB1CC - AMB1PP | восстановление собственных векторов комплексной матрицы общего вида по заданным (с двойной точностью) собственным векторам матрицы, полученной в результате масштабирования исходной матрицы с помощью подпрограммы AMB1C (AMB1P) |
Вызываемые подпрограммы: нет
Замечания по использованию
| 1. |
В подпрограмме AMB1DD параметры SCALE и Z имеют тип DOUBLE PRECISION; | |
| 2. |
В подпрограмме AMB1CC (PP) собственные векторы задаются в
виде двух вещественных массивов ZR и ZI размерности
NM * M, в столбцах которых содержатся соответственно
вещественные и мнимые части собственных векторов
матрицы C (на входе) и матрицы A (на выходе).
Первый оператор подпрограммы AMB1CC
имеет вид: | |
| 3. | В подпрограмме AMB1PP параметры SCALE, ZR, ZI имеют тип DOUBLE PRECISION |
Подпрограмма: AFG7RR
Назначение
Вычисление собственных векторов вещественной матрицы общего вида по собственным векторам матрицы Хессенберга, полученной в результате применения к исходной матрице метода отражений (подпрограмма AFG7R)
Использование
SUBROUTINE AFG7RR (NM, LOW, IGH, A, ORT, M, Z)
Параметры
| NM - | число строк двумерных массивов A и Z, указанное при описании этих массивов в вызывающей подпрограмме (тип: целый); |
| LOW - IGH | простые переменные, имеют тот же смысл, что и 3 - ий и 4 - ый параметры подпрограммы AFG7R (тип: целый); |
| A - | вещественный двумерный массив размерности NM * IGH, выходной параметр подпрограммы AFG7R (см. описание 5 - го параметра подпрограммы AFG7R); |
| ORT - | вещественный вектор длины IGH, выходной параметр подпрограммы AFG7R (см. описание 6 - го параметра подпрограммы AFG7R); |
| M - | число столбцов двумерного массива Z (тип: целый); |
| Z - | вещественный массив размерности NM * M, содержащий в своих столбцах на входе в подпрограмму вещественные и мнимые части собственных векторов матрицы Хессенберга, полученной в результате применения метода отражения к исходной матрице A (подпрограмма AFG7R), а на выходе - соответствующие вещественные и мнимые части вычисленных собственных векторов матрицы A. |
Версии
| AFG7DD - | восстановление собственных векторов вещественной матрицы общего вида по заданным с двойной точностью собственным векторам матрицы Хессенберга, полученной в результате применения к исходной матрице метода отражений (подпрограмма AFG7D) |
| AFG7CC - | восстановление собственных векторов комплексной матрицы общего вида по заданным (с двойной точностью) собственным векторам матрицы Хессенберга, полученной в результате применения к исходной матрице метода отражений (подпрограмма AFG7C (AFG7P)) |
Вызываемые подпрограммы: нет
Замечания по использованию
| 1. |
В подпрограмме AFG7DD параметры A, ORT, Z имеют тип DOUBLE PRECISION; | |
| 2. |
Подпрограммы AFG7RR и AFG7DD не сохраняют вектор ORT; | |
| 3. |
Первый оператор подпрограммы AFG7CC имеет вид: | |
| 4. |
Подпрограмма AFG7PP имеет такие же параметры, как и подпрограмма AFG7CC, только при этом AR, AI, ZR, ZI, ORTR, ORTI имеют тип DOUBLE PRECISION; | |
| 5. | Подпрограммы AFG7CC и AFG7PP не сохраняют векторы ORTR, ORTI. |