Решается задача Коши для системы M уравнений
Y ' = F ( x, Y ) ,
Y ( xN ) = YN ,
Y = ( y1, ..., yM ) , F ( x, Y ) = ( f1 ( x, y1, ..., yM ), ..., fM ( x, y1, ..., yM ) ) .
Подпрограммы решения задачи Коши для нежестких уравнений и систем уравнений первого порядка охватывают наиболее распространенные классы методов численного интегрирования:
| - | класс одношаговых методов типа Рунге - Кутта, |
| - | класс многошаговых методов Адамса типа предиктор - корректоp и многозначный метод Гира, |
| - | класс экстраполяционных методов. |
Среди одношаговых методов Рунге - Кутта имеются:
| - | метод Хойна с пятью вычислениями правой части на шаге третьего порядка точности с оценкой погрешности по правилу Рунге [ 1, 2 ], |
| - | классический метод Рунге - Кутта с четырьмя вычислениями правой части четвертого порядка точности [ 1, 2, 3 ], |
| - | метод Mеpсона четвертого порядка точности с пятью вычислениями правой части на одном шаге [ 4 ], |
| - | метод Фельберга пятого порядка точности с шестью вычислениями правой части на одном шаге [ 5 ]. |
| - | метод Инглэнда пятого порядка точности с шестью вычислениями правой части на одном шаге [ 1, 15 ]. |
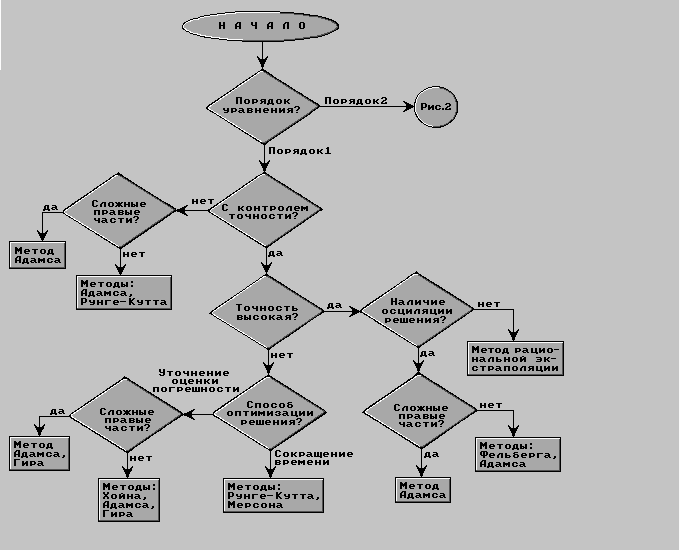
Правило Рунге и методы Фельберга и Инглэнда позволяют достаточно точно оценить погрешность приближенного решения на одном шаге, так как они используют оценку главного члена погрешности или оценку погрешности более высокого порядка (методы Фельберга и Инглэнда), чем классический метод Рунге - Кутта и метод Mеpсона. B тех случаях, когда предпочтительно сократить время счета и иметь невысокую точность приближенного решения, целесообразно использовать классический метод Рунге - Кутта и метод Mеpсона. Если важнее поточнее оценить погрешность, то следует пользоваться методами с более точной оценкой погрешности на шаге [ 18 ].
При громоздких правых частях, требующих выполнения большого числа арифметических операций, методы типа Рунге - Кутта могут потребовать много счетного времени для вычисления решения на всем интервале интегрирования. B этом случае более эффективными оказываются многошаговый метод Адамса пятого порядка [ 1, 2 ] и многозначный метод Гира переменного порядка [ 6 ], которые на одном шаге требуют значительно меньшего числа вычислений правой части. Для контроля точности приближенного решения в этих методах используется оценка главного члена погрешности, что позволяет довольно точно учитывать погрешность при малых размерах шага интегрирования [ 18 ].
Класс экстраполяционных методов представлен методом рациональной экстраполяции Грэгга - Булирша - Штера переменного порядка, в котоpом приближенные значения решения вычисляются с помощью явного метода прямоугольников второго порядка, которые затем уточняются с помощью рациональной экстраполяции Ричардсона [ 7, 8 ]. Получаемое таким способом повышение точности приближенного решения делает метод Грэгга - Булирша - Штера весьма эффективным методом в случае, когда требуется высокая точность приближенного решения.
Перечисленные в данном пункте методы имеют ограниченные области устойчивости, поэтому соответствующие им программы не эффективны и даже практически непригодны для жестких систем уравнений.
Hа pис.1 приводится дерево решений для выбора метода или группы методов численного интегрирования нежесткой задачи Коши.

Рис.1. Дерево решений для выбора метода интегрирования нежесткой задачи Коши