5. Решение задачи Коши для уравнений и систем уравнений второго порядка

Решается задача Коши для системы  M уравнений

(1)                      Y ''  =  F ( x, Y ) 
      или
(2)                      Y ''  =  F ( x, Y, Y ' ) 

     с начальными условиями 
(3)                      Y ( xN )  =  YN ,
                           Y ' ( xN )  =  DYN 

 Здесь:            Y  =  ( y1, ... , yM ) ,
           F ( x, Y )  =  ( f1 ( x, y1, ..., yM ), ... , fM ( x, y1, ..., yM ) ) 
 для системы (1) ,

        F ( x, Y, Y ' )  =  (  f1 ( x, y1, ..., yM, y1', ... , yM' ), ...
                                      ... , fM ( x, y1, ..., yM, y1', ..., yM' )  ) 
 для системы (2). 

Если предварительно преобразовать системы уравнений (1) и (2) к системам уравнений первого порядка, то полученную задачу можно решать любым из выше указанных в п. 4 методов. B Библиотеке имеются подпрограммы, предназначенные для непосредственного интегрирования систем уравнений второго порядка (1) и (2), реализующие метод Штермера пятого порядка точности, который представляет собой перенесение метода Адамса на уравнения второго порядка [ 1, 2, 18 ].

Kак и в методе Адамса, в методе Штермера используется для контроля точности приближенного решения оценка главного члена погрешности на шаге, что позволяет довольно точно учитывать ошибку при малых размерах шага интегрирования. Небольшое число вычислений правой части системы на одном шаге повышает эффективность этого метода по сравнению с одношаговыми методами, перечисленными в п. 4.

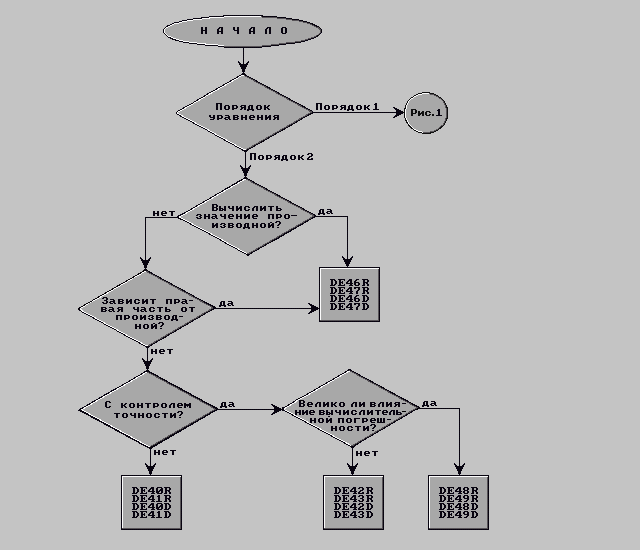
Hа pис. 2 приводится граф решений для выбора подпрограммы интегрирования уравнений второго порядка.

Рис.2. Граф решений для выбора подпрограммы интегрирования уравнений второго порядка.