К сожалению, решение нелинейных уравнений является исключительно сложным на практике. Применяемые методы являются существенно локальными и работают надежно лишь при наличии хороших начальных приближений. Заметим, однако, что такие "хорошие" начальные приближения вовсе не обязательно должны быть близкими к искомому решению.
Во всех предлагаемых в данном разделе подпрограммах желательно масштабировать задачу так, чтобы ненулевые компоненты решения были по абсолютной величине больше 0.1. При использовании подпрограмм в цикле или при их последовательном использовании следует не забывать при каждом повторном вхождении восстанавливать или заново определять значение ITMAX (максимальное число итераций, ориентировочно требуемых для обеспечения сходимости).
Следует иметь также в виду, что задание больших значений m (числа значащих цифр в приближенном значении решения) приводит к увеличению числа итераций и тем самым вычислений функций. В некоторых случаях ошибки округления при вычислениях функций делают невозможным достижение высокой точности. Тогда можно либо ослабить критерии сходимости, либо перейти к режиму вычислений с удвоенной точностью. Тем самым пользователь несет ответственность за установление значения m, которое является приемлемым для его задачи.
Среди трудностей, которые могут встретиться при решении нелинейных уравнений, наиболее существенным являются медленная сходимость к кратным или близким нулям, потеря точности при исключении найденного нуля перед поиском следующего, расхождение процесса при почти горизонтальных касательных или нахождение неправильного нуля при неудачном выборе критерия сходимости.
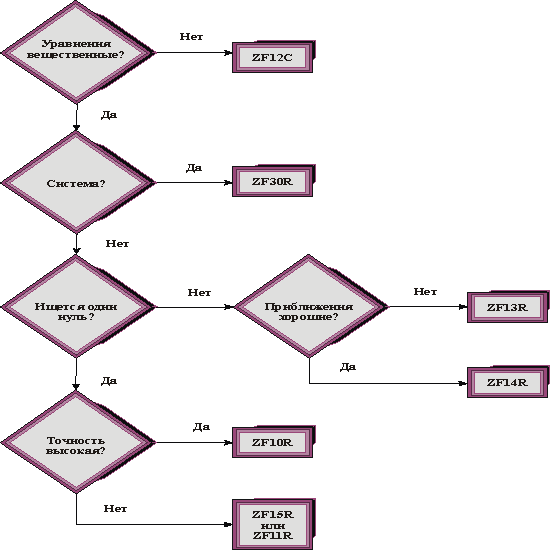
Из трех имеющихся подпрограмм на вычисление вещественного нуля вещественной функции подпрограмм ZF15R и ZF11R следует использовать для грубого нахождения нуля, тогда как ZF10R может быть выбрана для вычисления нуля с более высокой точностью.
При вычислении заданного числа нулей вещественной функции следует использовать подпрограмму ZF13R, когда заранее неизвестно, являются ли начальные приближения хорошими. Для уточнения найденных нулей при наличии хороших начальных значений может быть использована ZF14R.
Подпрограмма ZF12C (нули комплексной функции) показала высокие эксплуатационные качества и может быть использована для нахождения нулей вещественных и комплексных полиномов, если по каким - либо причинам возникают трудности при использовании более специальных подпрограмм раздела Библиотеки "Алгебра полиномов".
При использовании подпрограммы ZF30R при решении нелинейных систем можно получить дополнительные выгоды, если некоторые из уравнений системы окажутся линейными, однако, только в том случае, если они находятся в начале системы (чтобы добиться этого, можно перенумеровать уравнения).
Ниже приводится дерево решений для выбора необходимой подпрограммы с указанием ее имени по имеющимся данным о решаемой задаче.

| Рис. 1. | Дерево решений для выбора подпрограммы решения уравнений и систем общего вида. |