Как уже указывалось, программы Комплекса составлены на ФОРТРАНе - 77 в стиле SMPD (Single Program Multiple Data). Это означает, что одна и та же исполняемая программа загружается во все параллельные процессы, заказанные для решения задачи в команде запуска на счет. В то же время, каждый процесс занимается обработкой своих данных, составляющих некоторую часть общих данных задачи. Эти данные отдельного процесса (их называют локальными данными) непосредственно недоступны другим процессам и хранятся в отдельной (локальной) памяти каждого процесса. Необходимый обмен данными между разными процессами производится только посредством передачи сообщений (технология MPI [1, 2, 8, 9, 10, 11].
Из сказанного следует, что исходную матрицу A не
требуется хранить целиком в оперативной памяти
процессора как единый массив. На практике такие матрицы (векторы)
в виде единого целого могут храниться во внешних файлах (на дисковой
памяти). По этой причине такую матрицу A называют
глобальной матрицей.
Поскольку перед началом работы параллельных программ Комплекса исходные
глобальные матрицы (или векторы) разделяются на части и распределяются
по параллельным процессам,
то в дальнейшем нередко употребляется термин "распределенная
глобальная матрица (вектор)". Часть глобальной матрицы (вектора),
представленная в локальной памяти одного из параллельных процессов,
называется локальной частью матрицы (вектора). Совокупность всех
локальных частей на всех, используемых при решении задачи
параллельных процессах, и составляет распределенную глобальную
матрицу (вектор).
Поскольку каждый процесс работает со своей локальной частью данных (в нашем случае фрагментом глобальной матрицы), то в головной фортранной программе достаточно выделить (заказать) память, необходимую только для максимальной локальной части этой матрицы из всех локальных частей, обрабатываемых на параллельных процессах.
Локальные части, обрабатываемые на каждом из процессов, могут быть как одинакового, так и разного размера (см. подробнее пп.6.2,6.1). Для того чтобы каждый из процессов мог разместить свою локальную часть данных (матрицы), заказываемая область локальной памяти должна быть не меньше максимальной локальной части данных.
Таким образом, в головной фортранной программе, обращающейся к подпрограмме Комплекса, не требуется резервировать память для всего глобального объекта (матрицы или вектора) целиком, а только для их локальных частей.
Целиком эти объекты существуют, как правило, во внешних файлах. Для сохранения информации о конкретном способе разбиения глобального объекта на блоки и размещении блоков в локальной памяти всех процессов вводится объект, называемый дескриптором глобального массива. Дескриптор представляет собой одномерный массив, состоящий из 9 или 7 элементов (в зависимости от типа дескриптора). В дескрипторе хранится информация о размерах глобального массива (число строк и столбцов матрицы), о размерах блоков, на которые она разбивается, о номере процесса, в память которого распределяется первый блок глобальной матрицы (левый верхний угол), а также некоторая другая информация. Подробнее о дескрипторах см. в п.5.2.
По информации в дескрипторах, а также учитывая общие для Комплекса правила распределения блоков матриц (векторов) по параллельным процессам, всегда можно определить, в локальной памяти какого процесса и где именно находится элемент глобальной матрицы с глобальными индексами i и j. См. подробнее в п.6.1.
Непосредственно размещение исходных данных в локальной памяти каждого процесса должен выполнять сам пользователь (в головной программе, которая обращается к подпрограмме Комплекса) в соответствии с установленными в Комплексе правилами для матриц разных видов: плотных общего вида или симметричных, ленточных или трехдиагональных (см. п.6.3).
Организация решетки процессов, обмен информацией между процессами, а также другие действия, связанные с процессами, выполняются с помощью подпрограмм пакета BLACS. Пользователю, однако, в большинстве случаев не требуется знание всех возможностей этого пакета. При решении одной из задач линейной алгебры он должен сделать в головной программе лишь несколько стандартных обращений к нескольким подпрограммам пакета BLACS. Наглядные примеры этого можно найти, например, в предлагаемом пользователям описании целевой параллельной подпрограммы Комплекса (в разделе "Пример использования", см. во второй части методического пособия Приложение 2_1), а также в фортранном тексте тестового примера к этой подпрограмме (см. Приложение 2_2). Более подробно описание решеток процессов и правил работы с ними пользователей см. в пп.4, 6.1,6.2,5.2, и во второй части пособия 5,6.
Формальные параметры подпрограмм Комплекса могут быть глобальными или локальными. Глобальными называются параметры подпрограмм, которые относятся к указанным выше глобальным объектам. Например, глобальными являются число строк или столбцов исходной матрицы A (M, N) или число наддиагоналей (BWU) в A, если она является ленточной.
Локальными называются параметры, которые характеризуют объекты, определяемые в локальной памяти отдельного процесса. Например, указатель на локальную память, занимаемую локальной частью глобальной матрицы A или глобального вектора правых частей системы уравнений B.
Упоминавшиеся выше дескрипторы массивов характеризуются одновременно и как глобальные и как локальные параметры подпрограмм, поскольку среди их элементов, определяющих в основном характеристики глобальных массивов, есть характеристика, описывающая размещение части глобального массива в локальной памяти процесса (ведущая размерность локального массива). Подробнее о параметрах см. п.5.3.
Как уже упоминалось выше пп. 4.2, 5.1, для каждого глобального массива (матрицы или вектора), который необходимо разбить на блоки (с последующим размещением каждого из них в локальной памяти параллельных процессов, участвующих в решении задачи), вводится специальный объект, называемый дескриптором массива. Дескриптор представляет собой одномерный массив, состоящий из 9 или 7 элементов целого типа (в смысле ФОРТРАНа). Он предназначен для хранения информации, конкретизирующей способ разбиения глобального массива на блоки и их распределение по всем параллельным процессам.
Дескрипторы являются обязательными параметрами целевых подпрограмм Комплекса.
Дескрипторы принято обозначать идентификатором DESC с добавлением в конце имени массива (матрицы или вектора). Например, DESCA означает дескриптор матрицы A, DESCB - дескриптор вектора B.
Дескрипторы бывают трех типов, которые обозначаются целыми числами: 1, 501, 502.
5.2.1. Для плотных глобальных матриц A, которые распределяются по двумерной решетке процессов, используется дескриптор, имеющий тип 1 и состоящий из 9 элементов, за каждым из которых закреплено свое символическое имя (см. таблицу ниже). В таблице указываются номер (индекс) каждого элемента в массиве, его символическое имя (которое оканчивается символом подчеркивания "_" ), а также его смысл. Идентификатор, стоящий в символическом имени элемента после символа подчеркивания "_", является идентификатором глобального массива, описываемого данным дескриптором. Например, N_A обозначает элемент дескриптора, который содержит число столбцов глобальной матрицы A.
| N | Имя | Смысл | |
|---|---|---|---|
| 1. | DTYPE_A | - | тип дескриптора (для плотной матрицы A DTYPE_A = 1) |
| 2. | CTXT_A | - | обозначение контекста BLACS'а, сооветствующего выбранной решетке процессов, по которой распределяется глобальная матрица A. Целое значение, устанавливаемое подпрограммой из пакета BLACS. См. п.4. |
| 3. | M_A | - | число строк в глобальной матрице A |
| 4. | N_A | - | число столбцов в глобальной матрице A |
| 5. | MB_A | - | число строк в блоках, на которые разбивается глобальная матрица A |
| 6. | NB_A | - | число столбцов в блоках, на которые разбивается глобальная матрица A |
| 7. | RSRC_A | - | номер строки процесса в решетке процессов, куда был распределен первый элемент глобальной матрицы A (левый верхний угол); как правило удобнее всего распределять первый элемент в процесс с номером (0,0) |
| 8. | CSRC_A | - | номер столбца процесса в решетке процессов, куда был распределен первый элемент глобальной матрицы A (левый верхний угол); как правило удобнее всего распределять первый элемент в процесс с номером (0,0) |
| 9. | LLD_A | - |
ведущая размерность локального массива ( LLD_A і MAX(1, LOCr(M_A)), см. пояснения ниже в п.5.2.2. |
Например, записи DESCA(3) и DESCA(M_A) означают один и тот же элемент дескриптора матрицы A , содержащий число строк этой матрицы.
Для ленточных и трехдиагональных глобальных матриц A, которые распределяются по решетке процессов вида 1 * P , используются дескрипторы, имеющие тип, который обозначается целым числом 501, и состоящие из 7 элементов. Описание этих дескрипторов приводится в Приложении 1_1.
Подробнее о правилах распределения глобальных матриц по процессам см. в пп.6.1,6.2, и во второй части пособия пп. 5, 6.
5.2.2. Некоторых пояснений требует элемент дескрипторов, называемый ведущей размерностью локального массива и имеющий символическое имя LLD_ (для глобальной матрицы A обозначаемый LLD_A). Он является девятым элементом в дескрипторах типа 1 и шестым элементом в дескрипторах типа 501.
Как подробно описано в п.6.1 локальная часть (для некоторого процесса) плотной глобальной матрицы A, в общем случае, представляет из себя двумерный массив, составленный из нескольких циклически распределенных блоков, на которые была разбита исходная матрица A. Эти блоки в исходной матрице A располагались на расстоянии друг от друга (т.е. не примыкали один к другому). В локальной части матрицы A все циклически распределенные на данный процессор блоки плотно примыкают друг к другу, образуя единый сплошной двумерный массив. Элементы этого массива, как и положено в языке ФОРТРАН, располагаются в локальной памяти процесса по столбцам. Значение ведущей локальной размерности LLD_ задает число элементов в таком столбце, т.е., по - другому, число строк в локальном массиве (локальной части матрицы A). Число строк локального массива обозначается LOCr (M_A).
Поясним сказанное на наглядном простом примере.
Пусть матрица разбивается на одинаковые блоки так, что элементы строки
попадают в три блока, из которых последний (правый) блок содержит меньше
элементов, чем предыдущие слева от него (т.к., в общем случае, длина строки
матрицы не делится нацело на длину строки блока). А элементы столбца матрицы
попадают в три блока с одинаковым количеством элементов столбца. Представим это
на картинке ниже, обозначив каждый из блоков матрицы двойным номером (индексом).
|-----------|-----------|-------|
| | | |
| 11 | 12 | 13 |
| | | |
|-----------|-----------|-------|
| | | |
| 21 | 22 | 23 |
| | | |
|-----------|-----------|-------|
| | | |
| 31 | 32 | 33 |
| | | |
|-----------|-----------|-------|
Теперь распределим в соответствии с принятыми правилами эти блоки по параллельным процессам ( начиная с процесса с номером (0,0) ), предположив, что у нас имеется 4 процесса, образующие решетку ( 2, 2 ). При правильном распределении процесс с номером (0,0) будет содержать массив, составленный из следующих блоков.
|-----------|-------|
| | |
| 11 | 13 |
| | |
|-----------|-------|
| | |
| 31 | 33 |
| | |
|-----------|-------|
Процесс с номером (0,1) будет содержать, следующий массив из блоков.
|-----------|
| |
| 12 |
| |
|-----------|
| |
| 32 |
| |
|-----------|
Процесс с номером (1,0) - массив из блоков:
|-----------|-------|
| | |
| 21 | 23 |
| | |
|-----------|-------|
Процесс с номером (1,1) - массив из одного блока.
|-----------|
| |
| 22 |
| |
|-----------|
Как видим, если распределение начинается с блока с номером (0,0), он будет содержать наибольшее число элементов исходной матрицы. Т.о. максимальная ведущая размерность локального массива у массива на процессе с номером (0,0) и равна сумме строк в блоках 11 и 31 (в нашем случае она также равна ведущей размерности локального массива на процессе с номером (0,1), равной сумме строк в блоках 12 и 32).
Рассмотрим, как можно вычислить число строк или столбцов в локальной части матрицы A для некоторого процесса.
Пусть K будет числом строк (или столбцов) глобальной матрицы, и предположим, что решетка процессов, по которой матрица распределяется, имеет размерность NPROW * NPCOL.
LOCr (K) означает число строк из общего числа K, которое получит процесс, если K было распределено по NPROW процессам из столбца этой pешетки процессов (составляющим столбец этой pешетки).
Подобным образом, LOCc (K) означает число столбцов из общего числа K, которое получит процесс, если K было распределено по NPCOL процессам, составляющим строку этой pешетки.
Значения LOCr ( ) и LOCc ( ) для некоторого процесса с координатами в pешетке процессов (MYROW, MYCOL) можно определить посредством вызова служебной функции (tool function) NUMROC.
LOCr(M) = NUMROC(M, MB_A, MYROW, RSRC_A, NPROW), LOCc(N) = NUMROC(N, NB_A, MYCOL, CSRC_A, NPCOL).
Верхнюю границу для этих величин можно вычислить следующим образом:
LOCr(M) Ј ceil( ceil(M / MB_A) / NPROW) * MB_A LOCc(N) Ј ceil( ceil(N / NB_A) / NPCOL) * NB_A
Таким образом ведущая размерность исходной матрицы A LLD_A равна максимальному числу строк в локальной части матрицы среди всех локальных частей этой матрицы.
Правила разбиения и распределения по процессам глобального вектора (или матрицы) правых частей систем линейных уравнений B рассматриваются во второй части методического пособия в п.3.
Поскольку дескрипторы являются обязательными входными параметрами при обращении к целевым программам Комплекса, инициализировать дескрипторы (т.е. присвоить значения их элементам) необходимо до обращения к целевым программам. Для плотных матриц, распределение которых описывается дескрипторами типа 1, инициализацию проще всего выполнить с помощью специальной служебной подпрограммы Комплекса с именем DESCINIT, которой в качестве параметров необходимо передать значения всех элементов дескриптора. В п.4.2. приводятся примеры обращения к этой подпрограмме при инициализации дескриптора DESCA для плотной матрицы A. Пример обращения к этой подпрограмме при инициализации дескриптора DESCB для вектора (матрицы) правых частей систем линейных уравнений B приводится во второй части методического пособия в п. 3. Примеры инициализации дескрипторов DESCA и DESCB, имеющих типы 501 и 502, можно найти в разделе "Пример использования" описания одной из подпрограмм для решения систем с ленточной матрицей A.
После того как пользователь проделал работу по распределению глобальных матриц по процессам, он может обратиться к одной из подпрограмм Комплекса для выполнения необходимых операций над этими матрицами. Для правильного задания фактических параметров пользователь должен ознакомиться с описанием подпрограммы (т.е. с инструкцией по её использованию). К описанию целевой подпрограммы Комплекса можно обратиться с одной из страниц Систематического каталога
Одна из особенностей подпрограмм Комплекса состоит в том, что они допускают возможность обработки не только всей распределенной матрицы, но и некоторой ее части, называемой подматрицей (без необходимости заново проделывать работу по перераспределению этой подматрицы по процессам). Для этого, в частности, в подпрограммах были введены два дополнительных параметра.
IA - номер строки исходной распределённой глобальной матрицы А,
в которой находится первый элемент подматрицы,
JA - номер столбца исходной распределённой глобальной матрицы А,
в котором находится первый элемент подматрицы
Скорее всего возможность работы с подматрицами уже распределённой глобальной матрицы будет использоваться достаточно редко. При работе с полными матрицами параметры IA и JA будут полагаться равными 1, что упрощает читабельность и использование подпрограмм.
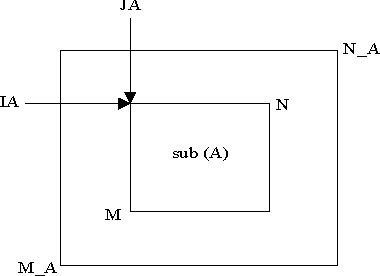
Тем не менее, для наглядности представим на рисунке исходную глобальную матрицу A и выделенную пользователем подматрицу sub (A), которая предназначена для обработки подпрограммой Комплекса.

В документации к программному Комплексу (в том числе и в описаниях подпрограмм) указанная на рисунке подматрица распределенной матрицы A(M_A, N_A) обозначается либо как sub (A), либо как A (IA: IA + M - 1, JA: JA + N - 1), т.е. с явным указанием положения этой подматрицы внутри исходной матрицы и ее размеров.
Для работы с подматрицами исходных матриц необходимо задать их характеристики в списках параметров подпрограмм Комплекса.
Для случая плотных матриц таких параметров шесть:
Имена индексов строки и столбца глобального массива имеют форму I<имя_массива> и J<имя_массива> соответственно. Дескриптор массива имеет имя в форме DESC<имя_массива>. Длина дескрипторного массива обозначается и определяется переменной DLEN_ и изменяется в зависимости от типа дескриптора DTYPE_ (подробное описание дескрипторов исходных распределенных матриц см. в п.5.2).
Пример описания параметров плотных матриц иллюстрируется ниже. Используемые здесь обозначения: M_A, N_A, LLD_A, LOCr( ), LOCc( ) объясняются при описании элементов дескриптора в п.5.2.
| М - | число строк подматрицы А(IA : IA+M-1, JA : JA+N-1), которая должна быть обработана; M і 0 и IA+M-1 Ј M_A (глобальный входной параметр, тип целый); |
| N - | число столбцов подматрицы А(IA : IA+M-1, JA : JA+N-1), которая должна быть обработана; N і 0 и JA+N-1 Ј N_A (глобальный входной параметр, тип целый); |
| А - | указатель на локальную часть распределенной глобальной матрицы с локальной размерностью (LLD_A, LOCc(JA+N-1)) (локальный входной и локальный выходной параметр, тип вещественный); |
| IA - | номер строки в глобальном массиве А, указывающий на первую строку подматрицы A(IA : IA+M-1, JA : JA+N-1) (глобальный входной параметр, тип целый); |
| JA - | номер столбца в глобальном массиве А, указывающий на первый столбец подматрицы A(IA : IA+M-1, JA : JA+N-1) (глобальный входной параметр, тип целый); |
| DESCA - | дескриптор распределенной глобальной матрицы А (т.е. одномерный дескрипторный массив длиной DLEN_ ); см. в п.5.2 (глобальный и локальный входной параметр, тип целый); |
Описание каждого параметра содержит следующую информацию:
Аналогичная информация для ленточных и трёхдиагональных матриц приводится в Приложении 1_2.